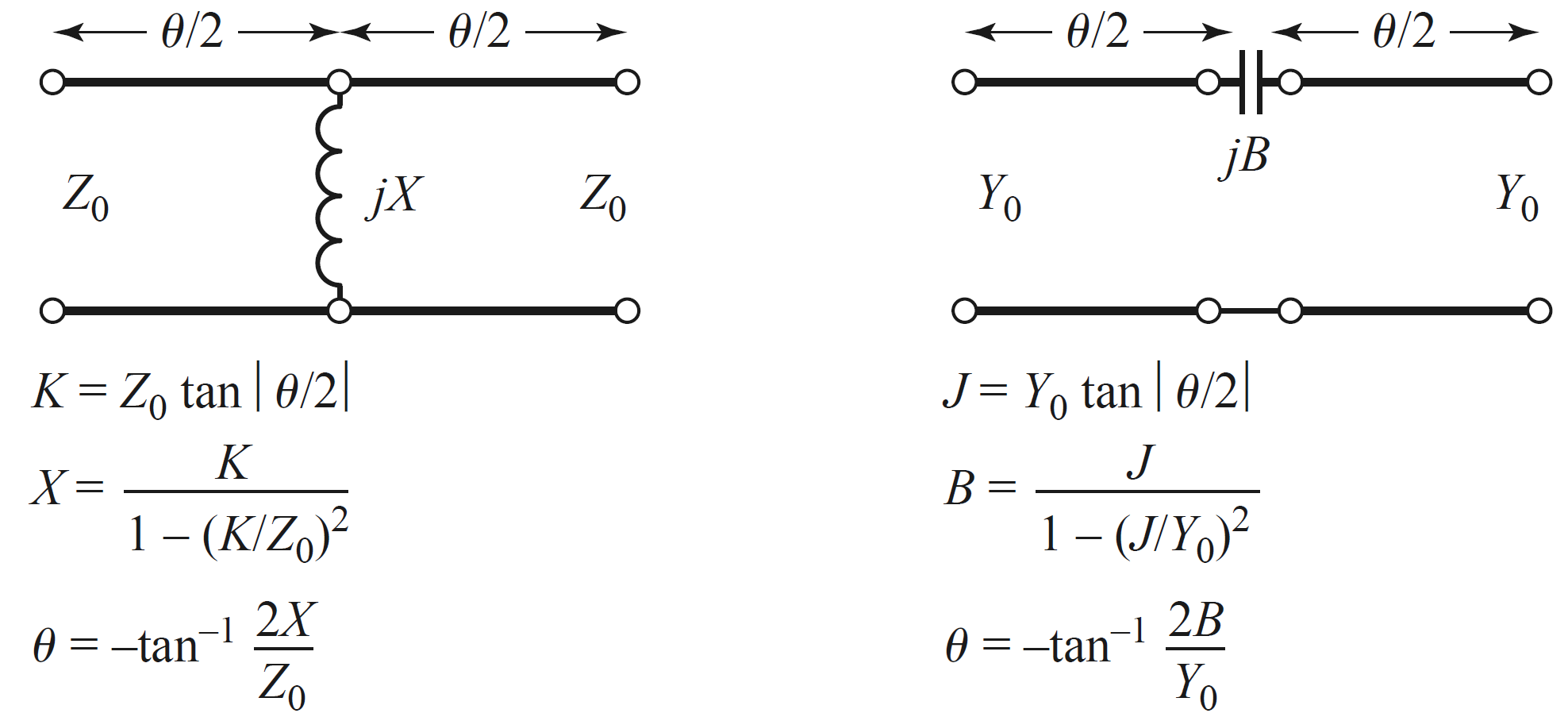RF滤波器设计笔记
本文记录在学习基本RF滤波器时所设计的微波理论。内容主要参考自《微波工程(第三版)》
微波网络分析
阻抗矩阵(Z矩阵)
对于一个N端口网络,阻抗矩阵([Z]矩阵)可由各端口的端口平面上的总电压和总电流确定,表达式如下:
$$ \begin{bmatrix} V_1 \\ V_2 \\ ... \\ V_N \end{bmatrix} = \begin{bmatrix} Z_{11} & Z_{12} & ... & Z_{1N} \\ Z_{21} & & & \\ ... & & ... & \\ Z_{N1} & & & Z_{NN} \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \\ ... \\ I_N \end{bmatrix} $$
其中,端口n的端口面的总电压为入射波电压与反射波电压之和:$V_n=V_n^++V_n^-$,总电流为入射波电流与反射波电流之差(由于方向性)$I_n=I_n^+-I_n^-$。上式中矩阵可简写为$[V]=[Z][I]$。
类似的,可以得到导纳矩阵(Y矩阵)表达式:$[I]=[Y][V]$,其中$[Y]$为$[Z]$互逆,即$[Y]=[Z]^{-1}$。
可利用下式计算Z矩阵中的元素:
$$Z_{ij}=\left.\frac{V_i}{I_j}\right|_{I_k=0,k\neq j}$$
即计算$Z_{ij}$时,通过给端口j施加激励电流$I_j$,并另所有其他端口开路,在端口i上测量其开路电压$V_i$即可。
类似的,可利用下式计算Y矩阵中的元素:
$$Y_{ij}=\left.\frac{I_i}{V_j}\right|_{V_k=0,k\neq j}$$
即计算$Y_{ij}$时,通过给端口j施加激励电压$V_j$,并另所有其他端口短路,在端口i上测量其短路电流$I_i$即可。
不含有非互易性介质(如有源器件、铁氧体等)组成的微波网络是互易的,其阻抗矩阵满足$[Z]=[Z]^T$。
对于无耗网络,网络的Z矩阵和Y矩阵必须为纯虚量,即各元素的实部均为0。
对于端口n,端口的输入阻抗即为$Z_{nn}$,注意输入阻抗可能会受其他端口的负载连接情况而影响。在端口接上特征阻抗为$Z_0$的传输线时,将端口的输入阻抗看作负载阻抗$Z_L$,传输线看入端口的反射系数为
$$\Gamma=\frac{Z_L-Z_0}{Z_L+Z_0}$$
散射矩阵(S矩阵)
对于一个N端口的网络,散射矩阵([S]矩阵)可由入射波和反射波电压振幅之间的关系确定:
$$ \begin{bmatrix} V_1^- \\ V_2^- \\ ... \\ V_N^- \end{bmatrix} = \begin{bmatrix} S_{11} & S_{12} & ... & S_{1N} \\ S_{21} & & & \\ ... & & ... & \\ S_{N1} & & & S_{NN} \end{bmatrix} \begin{bmatrix} V_1^+ \\ V_2^+ \\ ... \\ V_N^+ \end{bmatrix} $$
其中$V_n^+$时入射到端口n的电压波的振幅,$V_n^-$是自端口n反射回的电压波振幅。上式可简写为$[V^-]=[S][V^+]$。矩阵中个元素可由以下表达式确定:
$$S_{ij}=\left.\frac{V_i^-}{V_j^+}\right|_{V_k^+=0,k\neq j}$$
即在j端口输入激励信号$V_j^+$,其余端口无入射信号且端接匹配负载时,i端口的输出信号的电压(反射波电压$V_i^-$)与输入信号的比值,即为散射矩阵中相应元素的值。
对于2端口器件(如滤波器),可用$S_{11}$和$S_{22}$表征1端口和2端口的反射系数($\Gamma$),用$S_{21}$表征量端口之间的插入损耗。
传输矩阵(T矩阵、ABCD矩阵)
传输矩阵通常用于2端口网络,使用传输矩阵可以很容易地将多个网络级联起来。二端口网络的ABCD矩阵可由如下表达式定义:
$$ \begin{equation} \left\{ \begin{array}{lr} V_1=AV_2+BI_2 \\ I_1=CV_2+DI_2 \end{array} \right. \end{equation} $$
将其写为矩阵形式,为:
$$ \begin{bmatrix} V_1 \\ I_1 \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} V_2 \\ I_2 \end{bmatrix} $$
需要注意,与通常电流方向指向端口内为正方向不同,在传输矩阵地定义中,电流$I_2$的正方向定义为端口的出方向。如下图所示。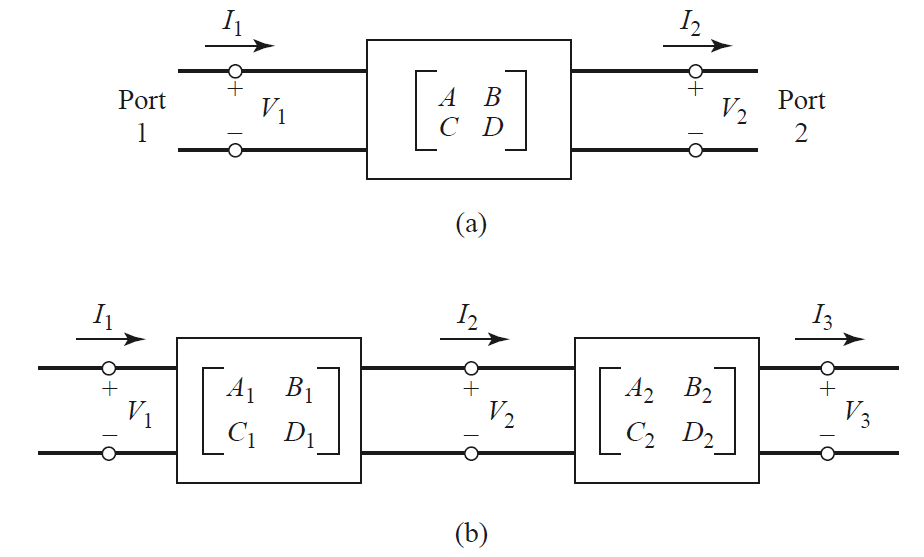
上图中,图(b)的整体可直接表示为:
$$ \begin{bmatrix} V_1 \\ I_1 \end{bmatrix} = \begin{bmatrix} A_1 & B_1 \\ C_1 & D_1 \end{bmatrix} \begin{bmatrix} A_2 & B_2 \\ C_2 & D_2 \end{bmatrix} \begin{bmatrix} V_3 \\ I_3 \end{bmatrix} $$
T矩阵中的参量可从其他矩阵转换过来,也可以直接计算。其中4个参量的表达式分别如下:
$$ \begin{equation} \left\{ \begin{array}{lr} A = \left.\frac{V_1}{V_2}\right|_{I_2=0} \\ B = \left.\frac{V_1}{I_2}\right|_{V_2=0} \\ C = \left.\frac{I_1}{V_2}\right|_{I_2=0} \\ D = \left.\frac{I_1}{I_2}\right|_{V_2=0} \\ \end{array} \right. \end{equation} $$
几种常见的结构的T矩阵如下所示。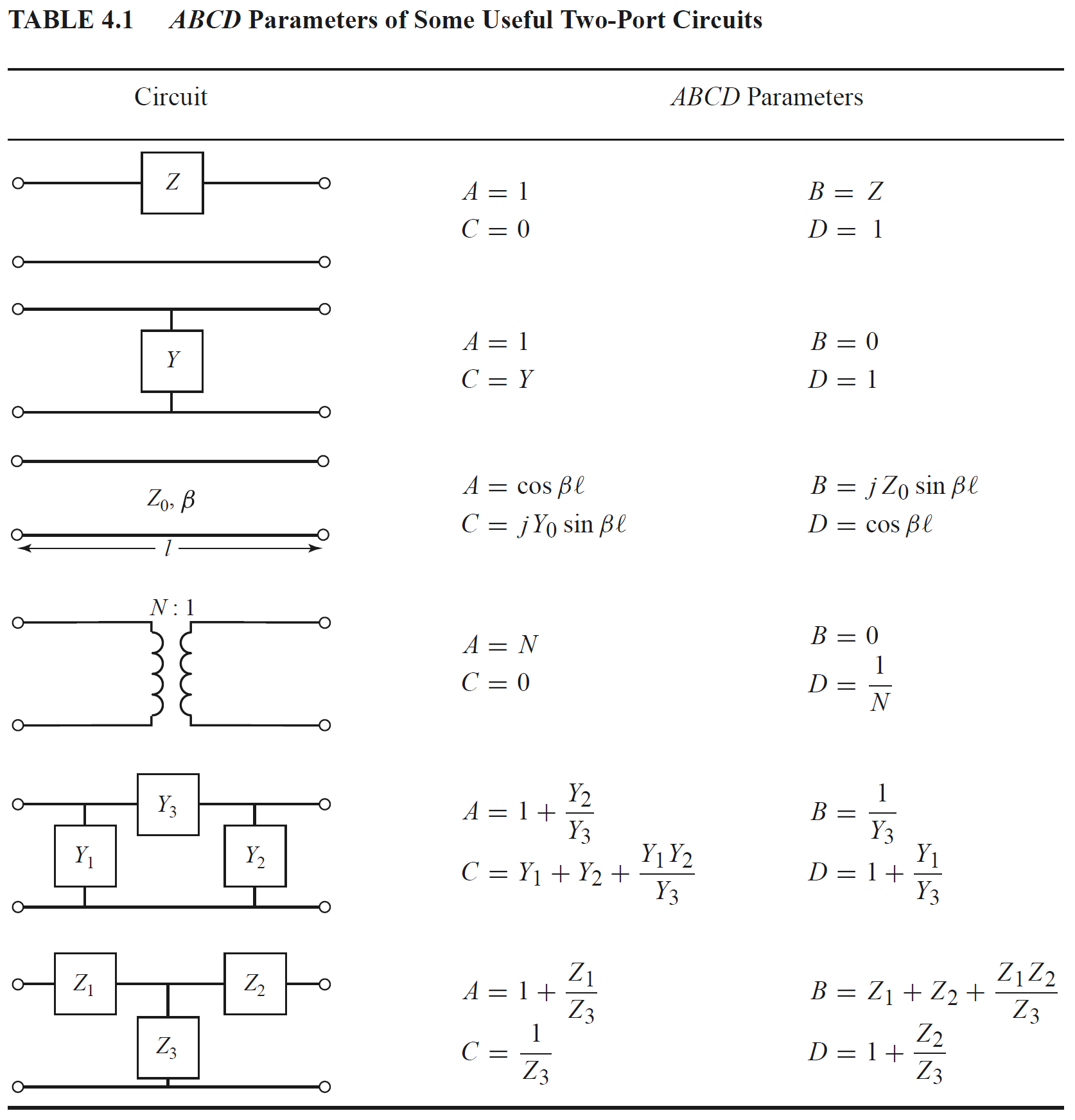
二端口网络各矩阵参量之间可以互相转换,转换关系如下所示(可查看原图)。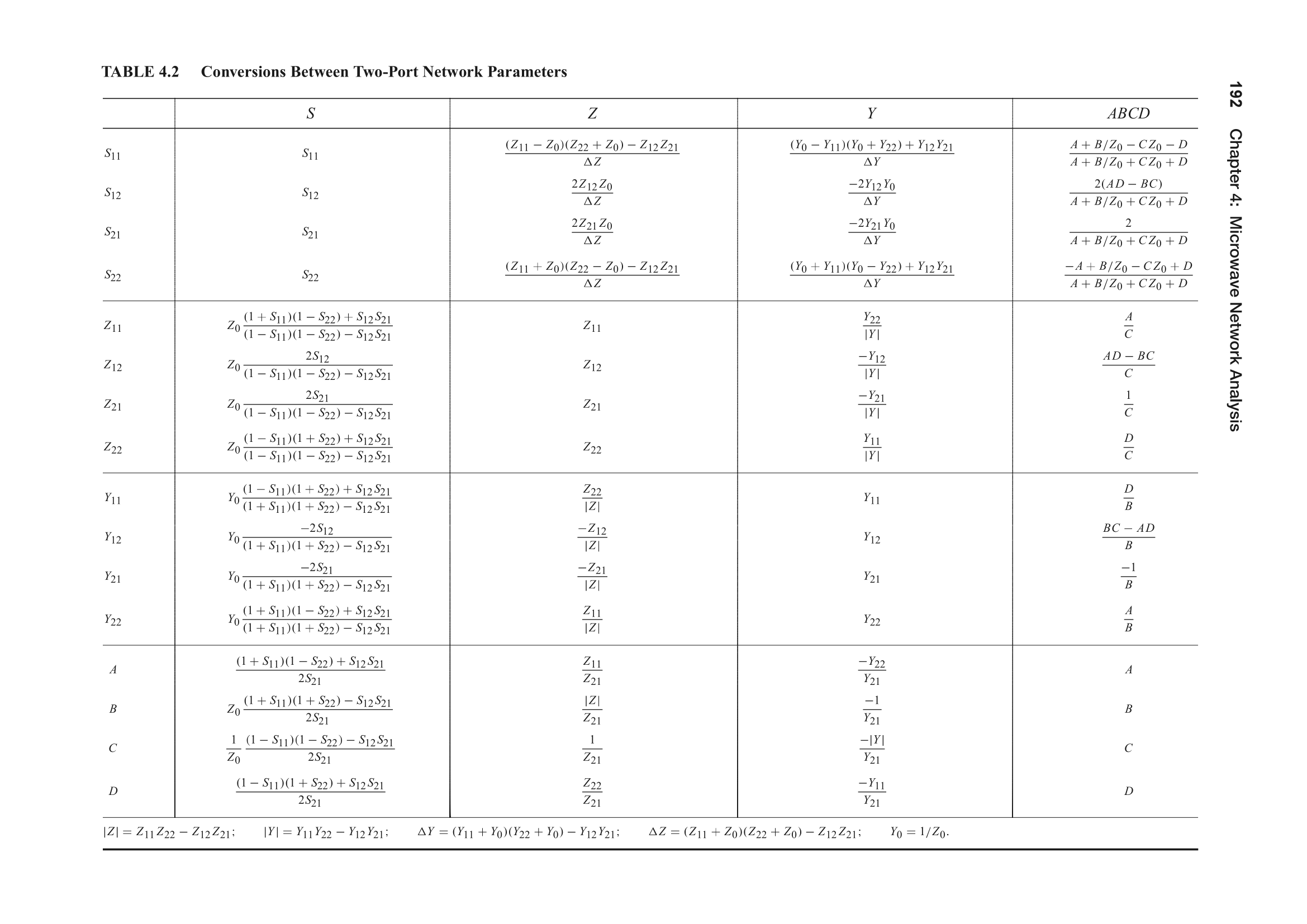
滤波器设计(插入损耗法)
滤波器分类
按频带特性分:低通滤波器(LPF)、高通滤波器(HPF)、带通滤波器(BPF)、带阻滤波器(BSF)
按插损响应特性分:最平坦滤波器(二项式滤波器、巴特沃斯滤波器 Butterworth Filter)、等纹波滤波器(切比雪夫滤波器 Chebyshev Filter)、椭圆函数滤波器(Elliptic Filter / Cauer Filter)、线性相位滤波器(最平坦时延迟滤波器、贝塞尔滤波器 Bessel Filter)。其他还有高斯滤波器(Gaussian Filter)、最佳L滤波器(Optimum "L" (Legendre) filter)、LR滤波器(Linkwitz–Riley Filter,为两个Butterworth Filter级联得到)。
滤波器的阻带衰减大致为每阶每10倍频向阻带外20dB。通常阶数越高,滤波器的理论特性越理想,但设计也越复杂,器件尺寸越大。
虽然最平坦滤波器在通带内可以得到理想的插损特性,但其通带附近的衰减斜率不及同阶的等纹波滤波器高,即等纹波滤波器虽然带内插损具有一定起伏,但具有较好的选择性。
滤波器设计
在选定滤波器阶数和类型后,先设计出低通滤波器原型,并选取对应的滤波器原型值${g_i}$。
各种不同响应类型的滤波器的低通原型值如下所示: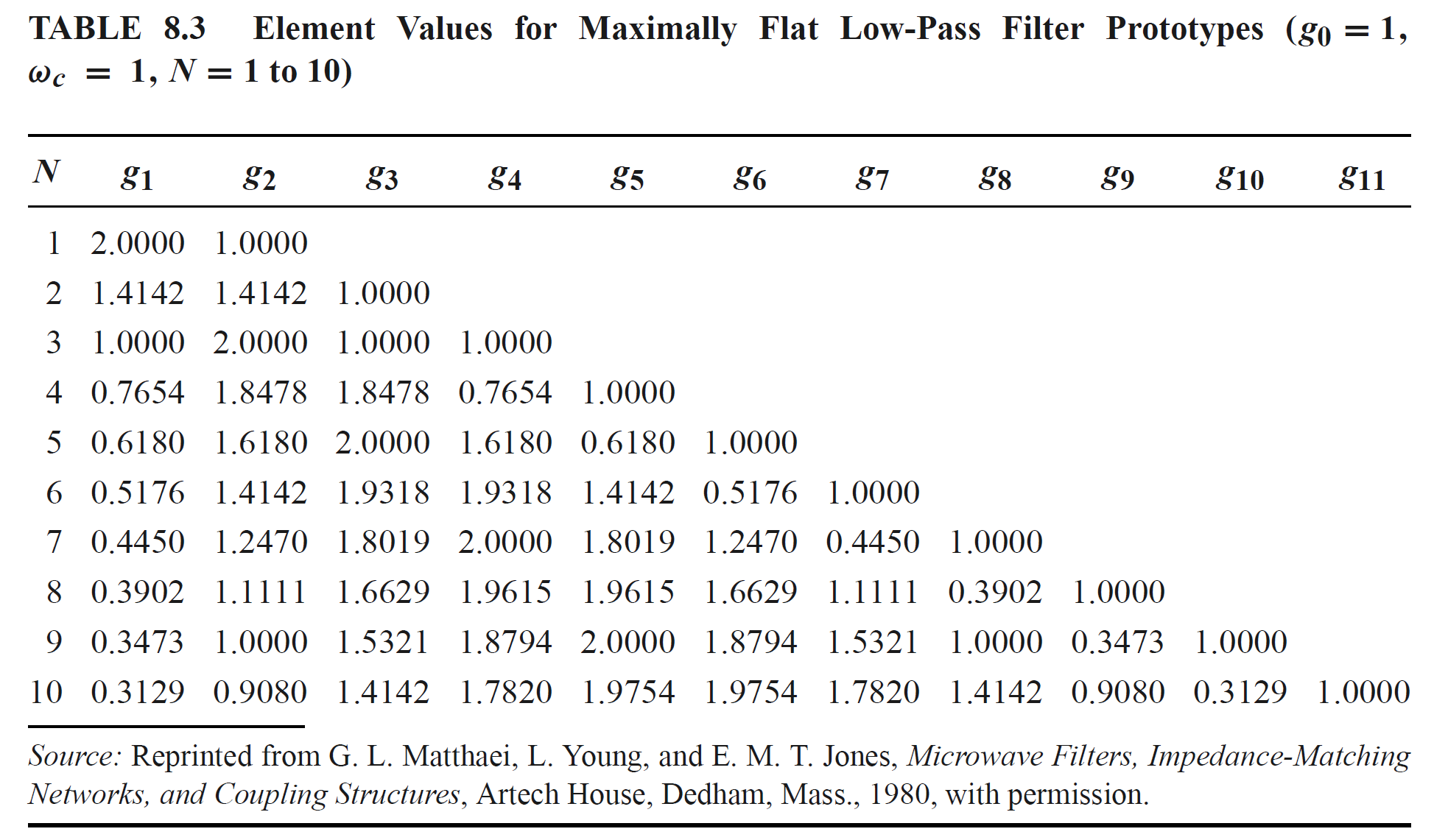
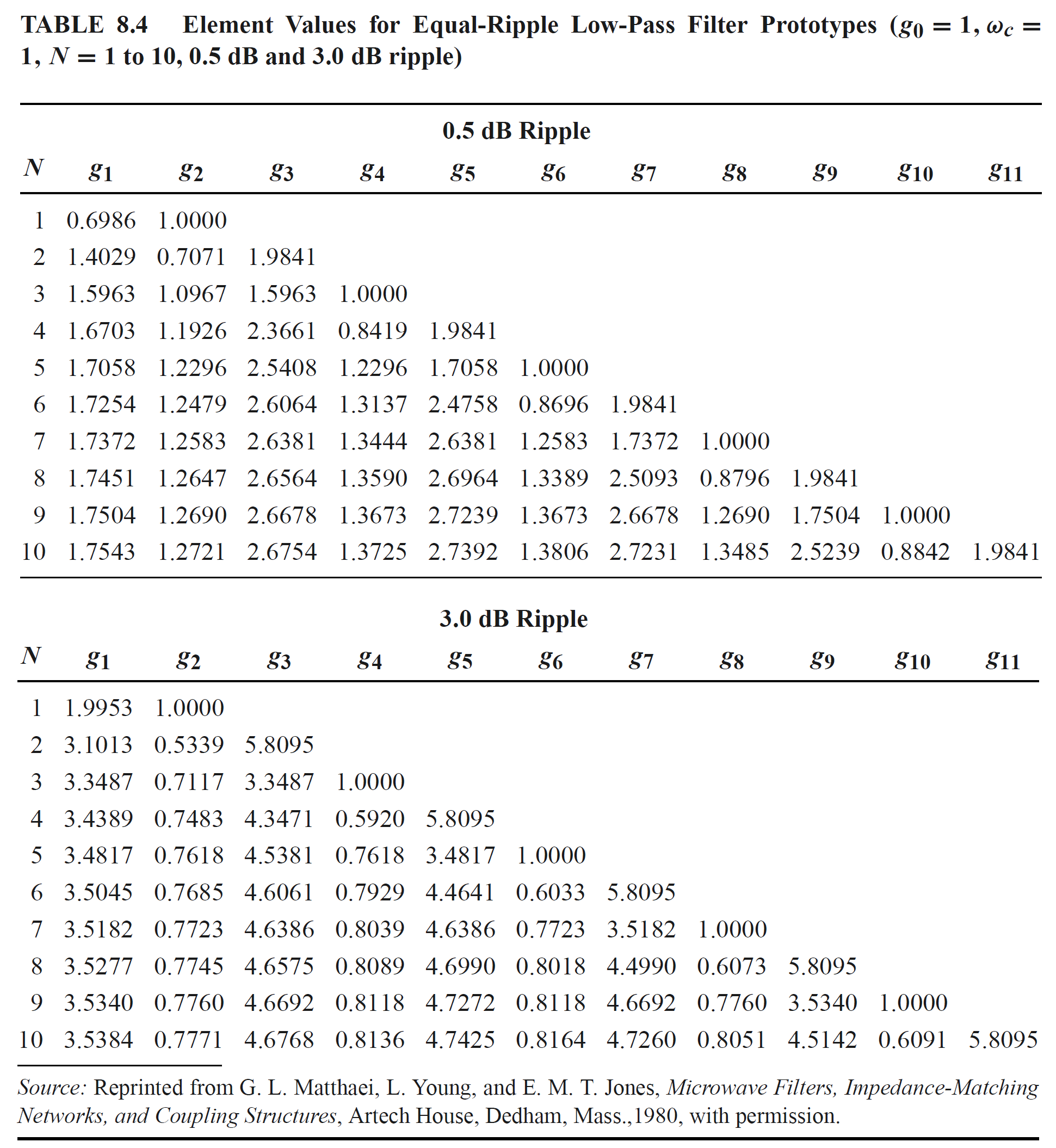
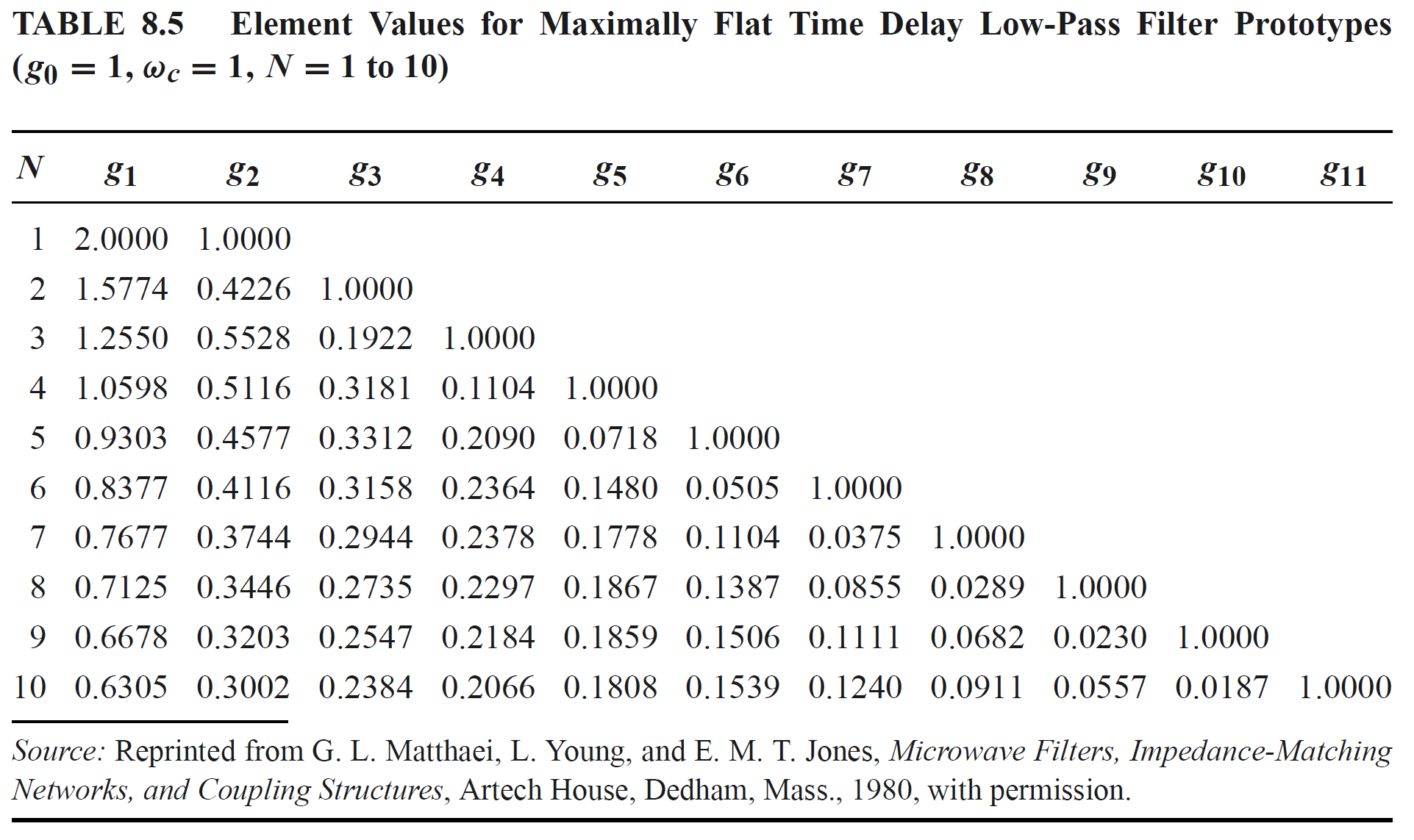
低通滤波器可以先从并联元件(并联电容)开始,也可以先从串联元件(串联电感)开始。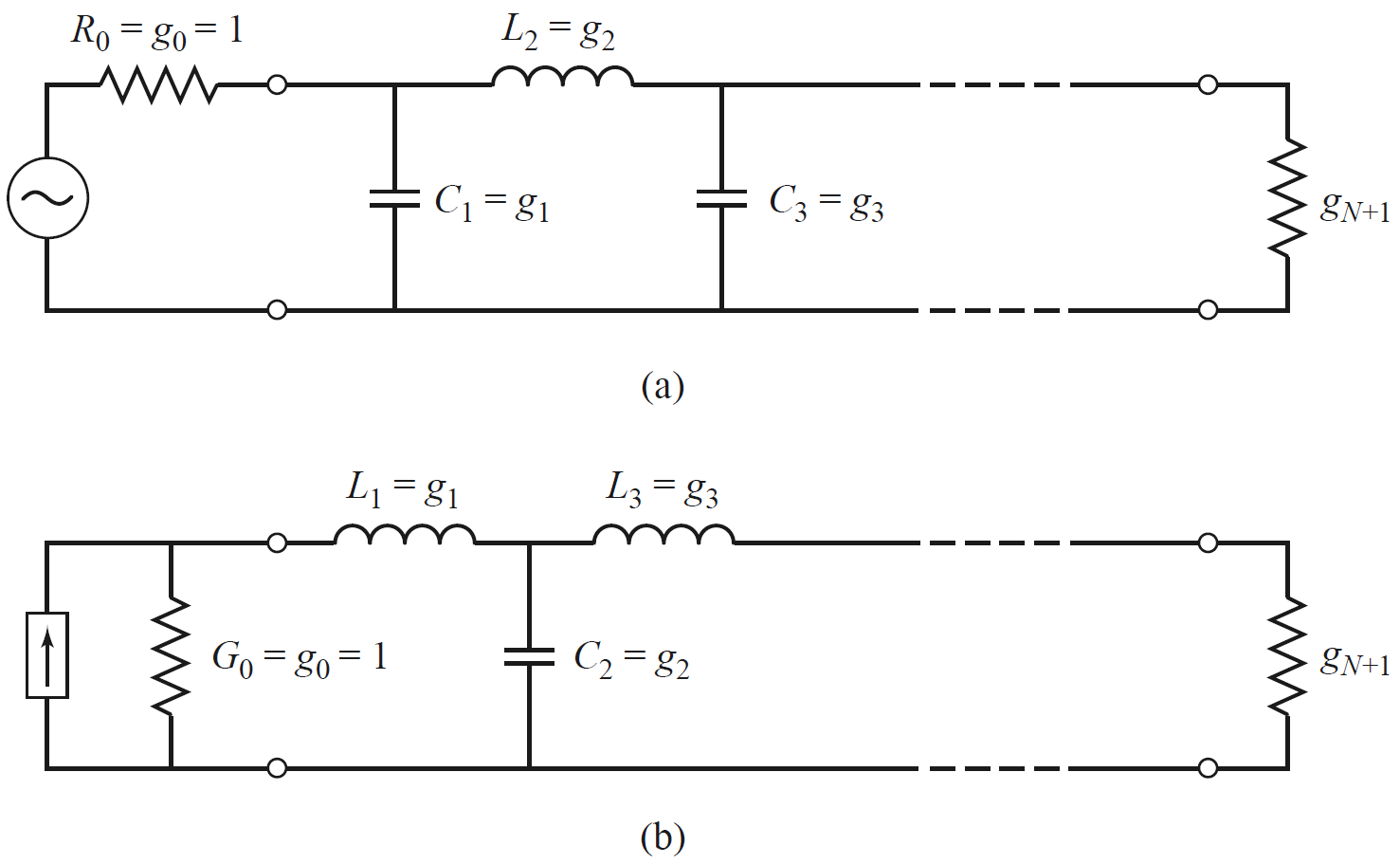
如果设计低通滤波器(LPF),则将原型值代入,并根据设计频率和特征阻抗,计算实际器件值即可。
如果设计其他类型的滤波器(HPF、BPF、BSF),则还需将各个原型元件转换成对应类型的元件组合。元件转换方式如下表所示。注意,其中转换得到的带通和带阻的一个原型元件变成了一对电容或电感的串联和并联,他们使用原型元件的同一个原型值。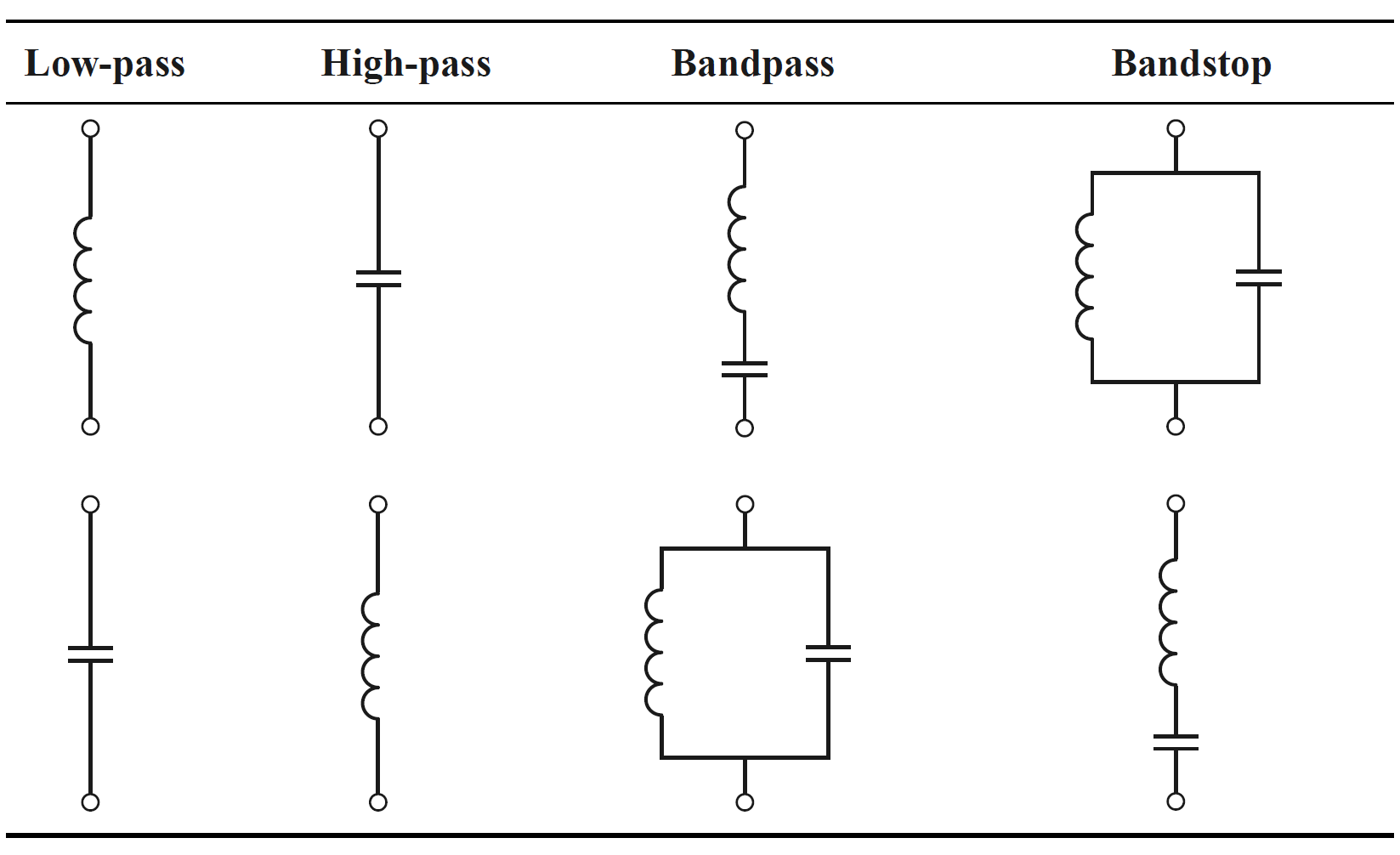
对应的实际元件值计算公式分别如下:
低通滤波器的电感:$$L_i=\frac{Z_0g_i}{\omega_c}$$
低通滤波器的电容:$$C_i=\frac{g_i}{Z_0 \omega_c}$$
高通滤波器中,电感原型变换为电容:$$C_i=\frac{1}{Z_0\omega_c g_i}$$
高通滤波器中,电容原型变换为电感:$$L_i=\frac{Z_0}{\omega_c g_i}$$
上述等式中,$\omega_c$为设计的截止频率(注意$\omega=2\pi f$),$Z_0$为端口阻抗。
带通滤波器中,电感原型变换为电感与电容串联:
$$ \begin{equation} \left\{ \begin{array}{lr} L = (Z_0g_i)/(\omega_0 \Delta) \\ C = \Delta/(\omega_0 Z_0 g_i) \\ \end{array} \right. \end{equation} $$
带通滤波器中,电容原型变换为电感与电容并联:
$$ \begin{equation} \left\{ \begin{array}{lr} L = (\Delta Z_0)/(\omega_0 g_i) \\ C = g_i/(\omega_0 \Delta Z_0 ) \\ \end{array} \right. \end{equation} $$
带阻滤波器中,电感原型变换为电感与电容并联:
$$ \begin{equation} \left\{ \begin{array}{lr} L = (g_i \Delta Z_0)/(\omega_0) \\ C = 1/(g_i \omega_0 \Delta Z_0 ) \\ \end{array} \right. \end{equation} $$
带阻滤波器中,电容原型变换为电感与电容串联:
$$ \begin{equation} \left\{ \begin{array}{lr} L = Z_0/(\omega_0 g_i \Delta) \\ C = (g_i \Delta)/(Z_0 \omega_0 ) \\ \end{array} \right. \end{equation} $$
上式中,$\omega_0$为中心频率,$\Delta$为相对带宽,其计算表达式为$\Delta=(\omega_2-\omega_1)/\omega_0$,即两个截止频率之差(通带或阻带的带宽)除以中心频率。
对于非低通滤波器,将低通滤波器原型的相应元件转换为该类型的相应元件或元件组合,并连接即可。之后利用变换后的元件的上述实际值计算公式,计算得到实际元件值,即可得到相应滤波器的集总参数元件设计。
设计与对比
设计截止频率为5GHz的低通滤波器,采用最平坦响应(Butterworth Filter)设计的2阶(即LC滤波器)、4阶滤波器,及4阶LR滤波器(2个2阶巴特沃斯滤波器直接级联)的原理图如下所示。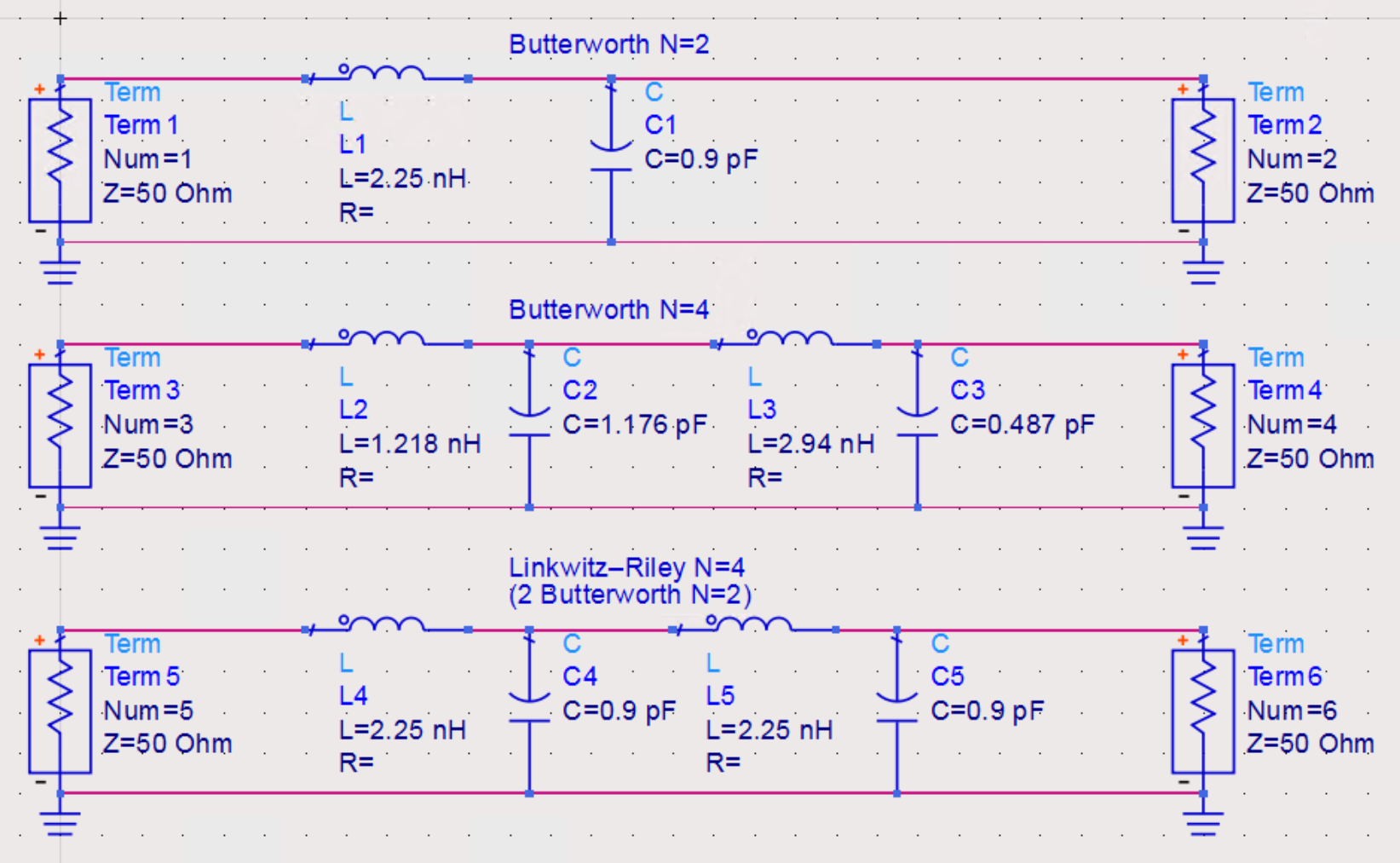
2阶(红线)、4阶(蓝线)滤波器的仿真的$S_{21}$参数结果如下。可以看出,2阶和4阶的截止频率均为5GHz,4阶滤波器的性能特性更接近理想低通滤波器。在通带外,2阶滤波器每10倍频衰减40dB,4阶滤波器每10倍频衰减80dB。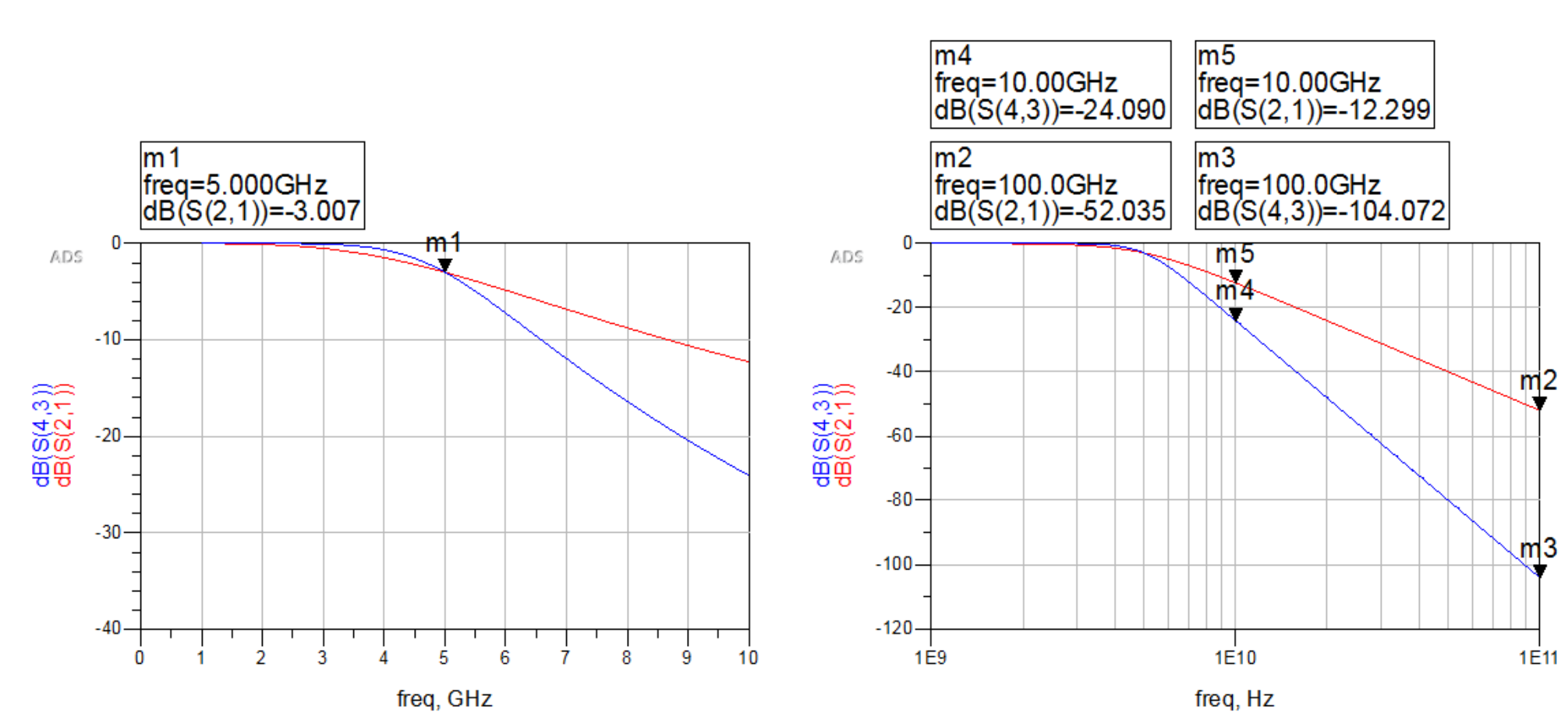
4阶最平坦滤波器(红线)和4阶LR滤波器(蓝线)的仿真的$S_{21}$参数结果如下。LR滤波器在5GHz处的插入损耗为0,但在通带内有近1dB的纹波,其通带宽向外延展。在高频段的阻带内,相同阶的LR滤波器比巴特沃斯滤波器有更高的阻带衰减。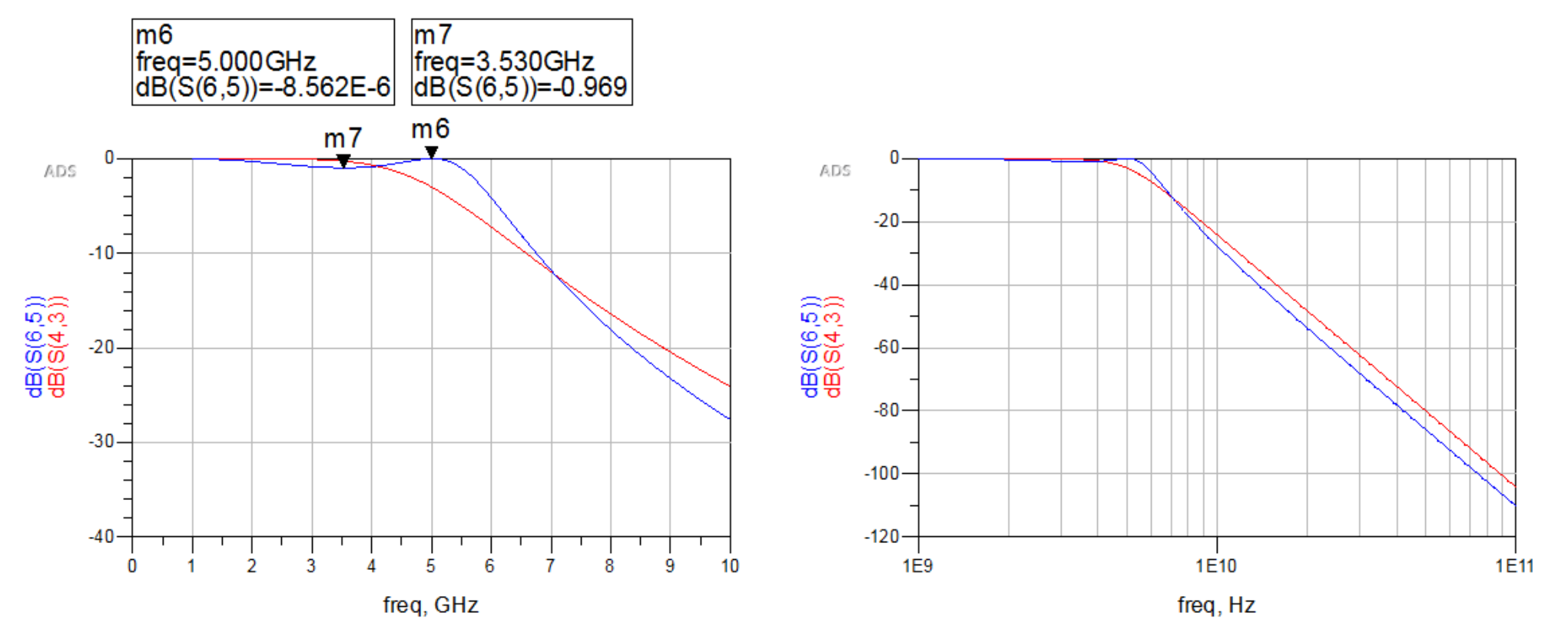
下图则是截止频率或中心频率在5GHz的4阶巴特沃斯滤波器的各种结构,其中BPF和BSF的相对带宽均为10%(BPF通带4.75GHz-5.25GHz,BSF阻带与之相同)。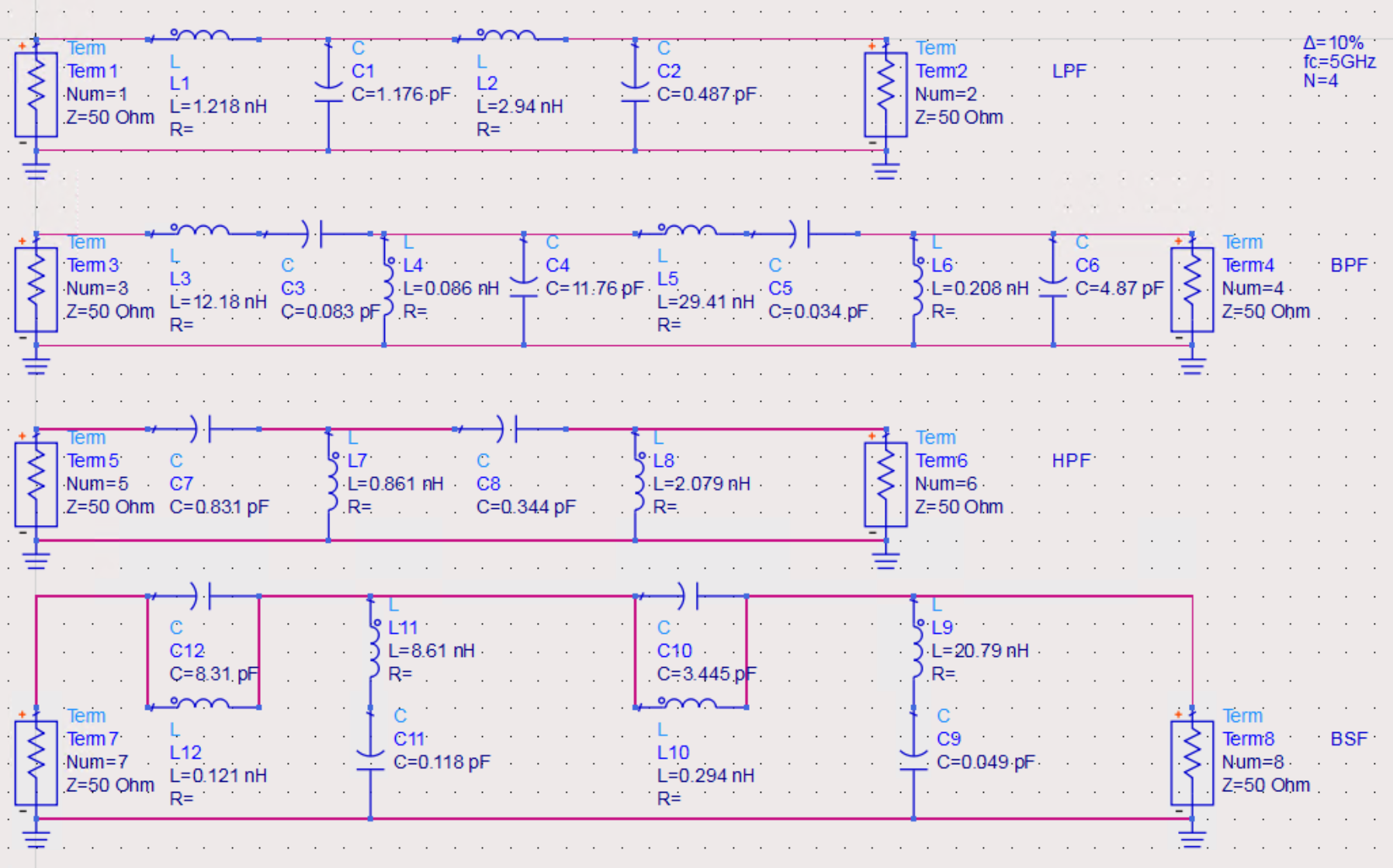
仿真的插入损耗结果如下所示。下图中,左图红线为LPF,蓝线为HPF;右图红线为BPF,蓝线为BSF。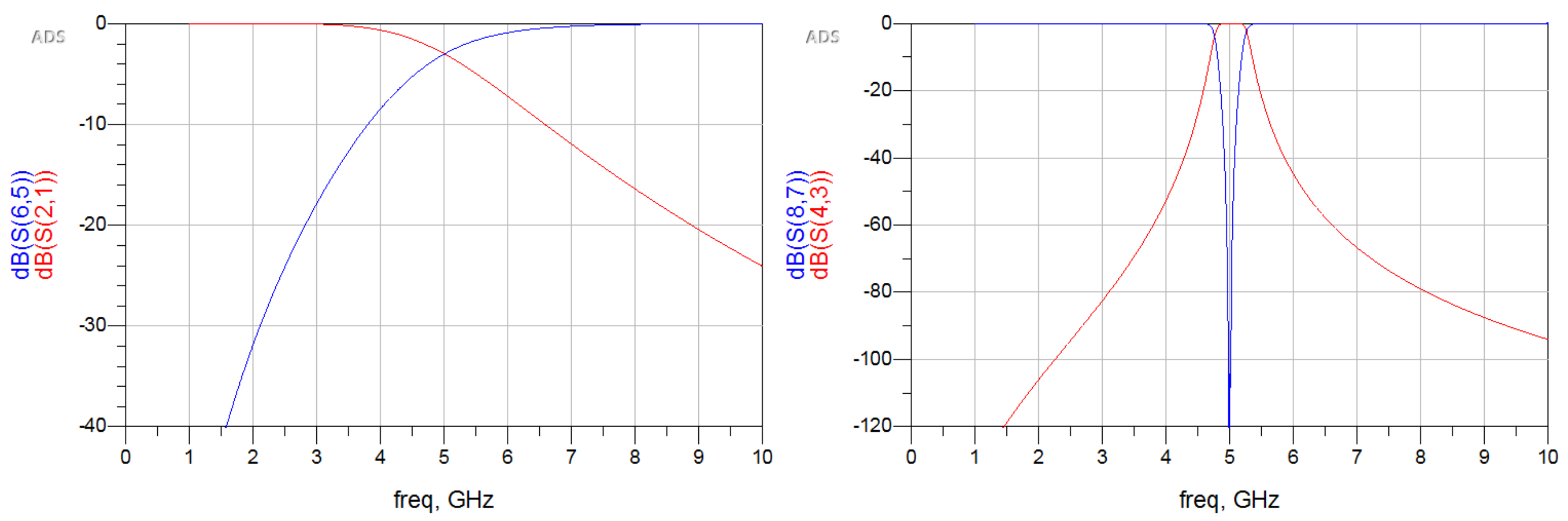
滤波器的微波电路实现
在微波频段,大体积的元件不可视为集总元件,小体积的元件则可能存在功率容量不足、稳定性不足等问题。通常,在平面结构的微波频段的滤波器电路中,电容电感会使用微带线实现。
理查德变换(Richards' Transformation)
集总元件滤波器设计中的电感和电容在原理可以用短路和开路短截线取代,这种线的长度都是相同的(在截止频率$\omega_c$处为$\lambda/8$),故又称为公比线。归一化电感量为$g$的电感可替换为电长度为$\lambda/8$、特征阻抗为$Z_0g$的短路线,归一化电容量为$g$的电容可替换为电长度为$\lambda/8$、特征阻抗为$Z_0/g$的开路线。
注意,这种等效通常只适用于并联元件,因为串联元件替换后得到的串联短截线在微带电路中通常是难以实现的。
科洛达恒等关系(Kuroda's Identities)
在低通滤波器和带阻滤波器中,可通过引入额外的不影响原本器件性能的传输线(如输入端和输出端增加相同阻抗的馈线),之后使用科洛达恒等关系将串联元件转换为并联元件。常用的两个转换关系如下: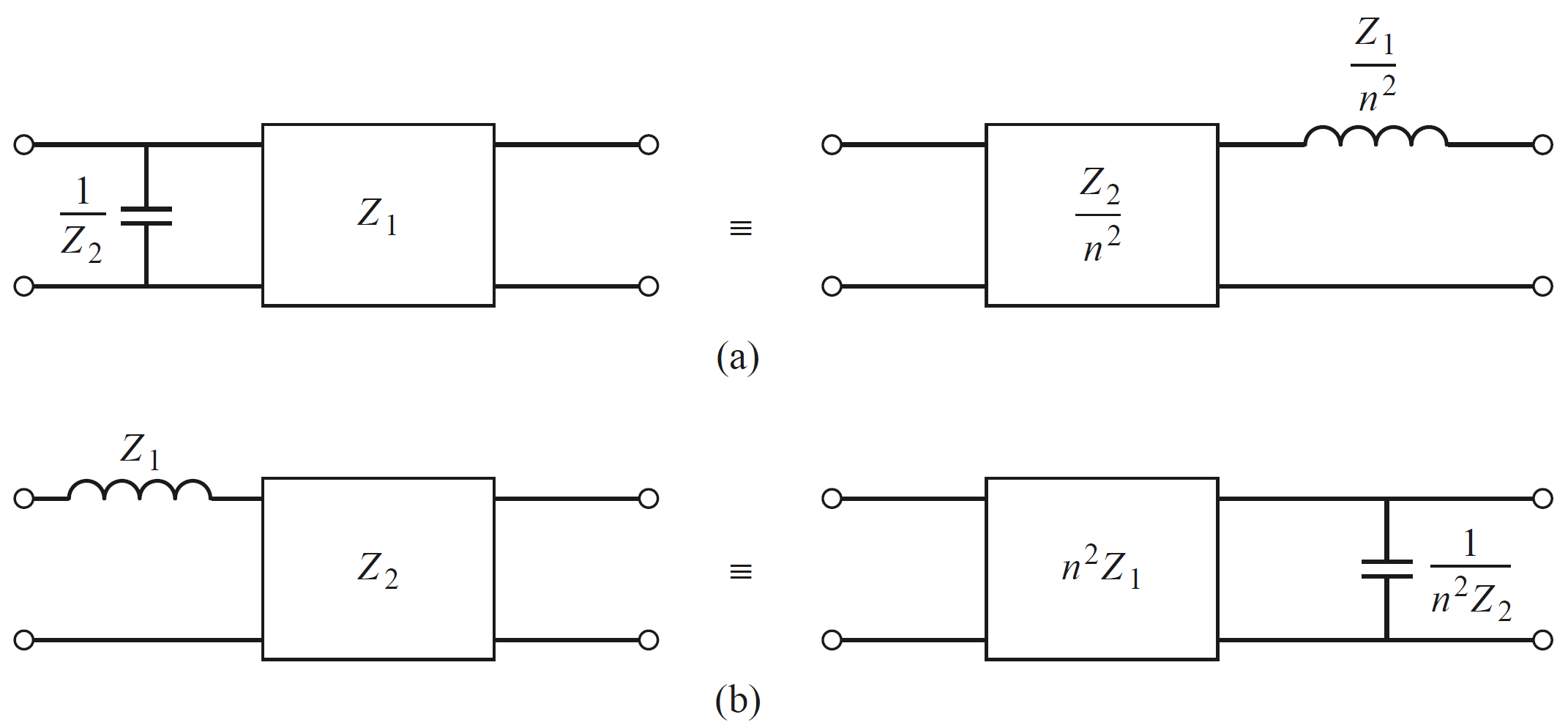
其中,方框代表电长度为$\lambda/8$的一段传输线,$n^2=1+Z_2/Z_1$。
短传输线等效
如果得到的传输线电长度小于$\lambda/8$,则可通过一段串联的高阻线(窄线)来等效串联的电感,通过一段串联的低阻线(宽线)来等效并联的电容。电感段的电长度为
$$\beta l=\frac{gZ_0}{Z_L}$$
其中,$g$为电感原型值,$Z_0$为等效后端口的特征阻抗,$Z_L$为用于等效电感的传输线的特征阻抗。可以通过调节传输线特征阻抗的宽度来调整合适的电长度。
电容段的电长度为
$$\beta l=\frac{gZ_C}{Z_0}$$
其中,$g$为电容原型值,$Z_C$为用于等效电容的传输线的特征阻抗。
四分之一波长传输线
四分之一波长传输线可以用于进行阻抗匹配(两个端口阻抗分别为$Z_1$和$Z_2$时,通过电长度为$\lambda/4$、特征阻抗为$Z=\sqrt{Z_1Z_2}$的传输线可以实现两个端口之间的匹配)。
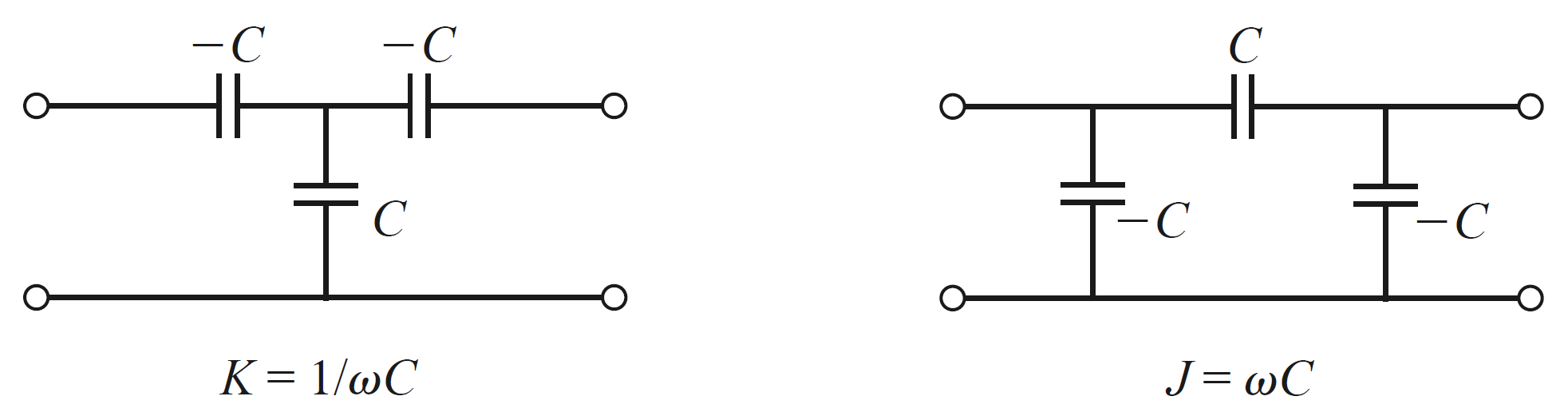
此外,四分之一波长的传输线还可以实现阻抗倒相器(Impedance Inverter)或导纳倒相器(Admittance Inverters)。如下图所示,使用一段特征阻抗为K(特征导纳为J)的电长度为$\lambda/4$的传输线可以将负载端口的阻抗形成反向,因此可用它们将串联元件变为并联元件,或实现一些通常其他方法难以直接得到的参数的元件。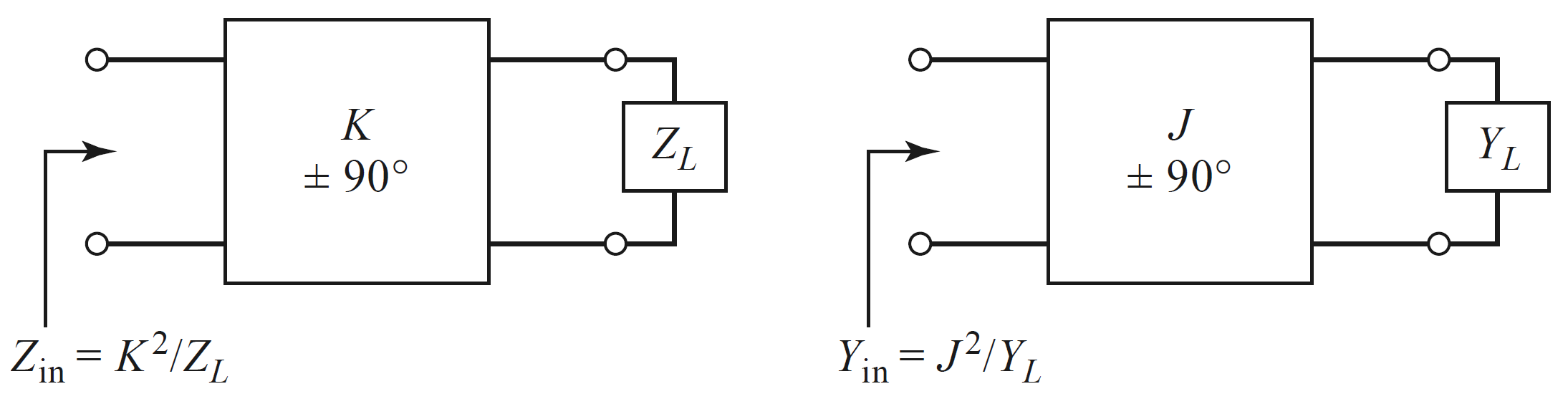
此外,利用电抗性元件和传输线、或用电抗网络也可以实现上图中K倒相器或J倒相器的功能。