椭圆函数滤波器设计

椭圆函数滤波器（Elliptic-function Filter）牺牲了带内和带外的平坦度，通过添加带外零点来显著提高滤波器过渡带的衰减速度。

翻了一圈，没有找到椭圆函数滤波器的设计方法，最后在Microstrip Filters for RF Microwave Applications (2nd Edition)中找到了，在此记录下，作为RF滤波器设计笔记的补充。

理论

椭圆函数低通滤波器具有如下图所示的插入损耗响应。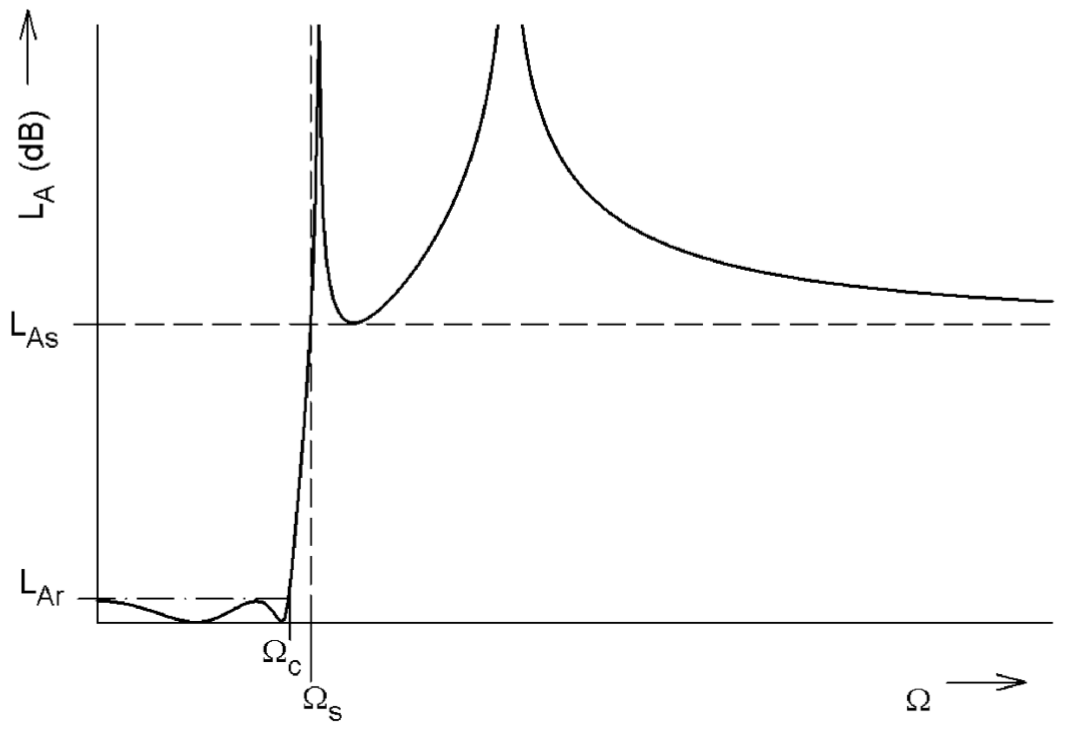

椭圆函数滤波器的低通原型主要有下面两种形式。显然，其中图(b)的形式很容易使用微带电路实现。对于奇数阶和偶数阶的滤波器，其差异只在最后是否需要多加入一个并联电容。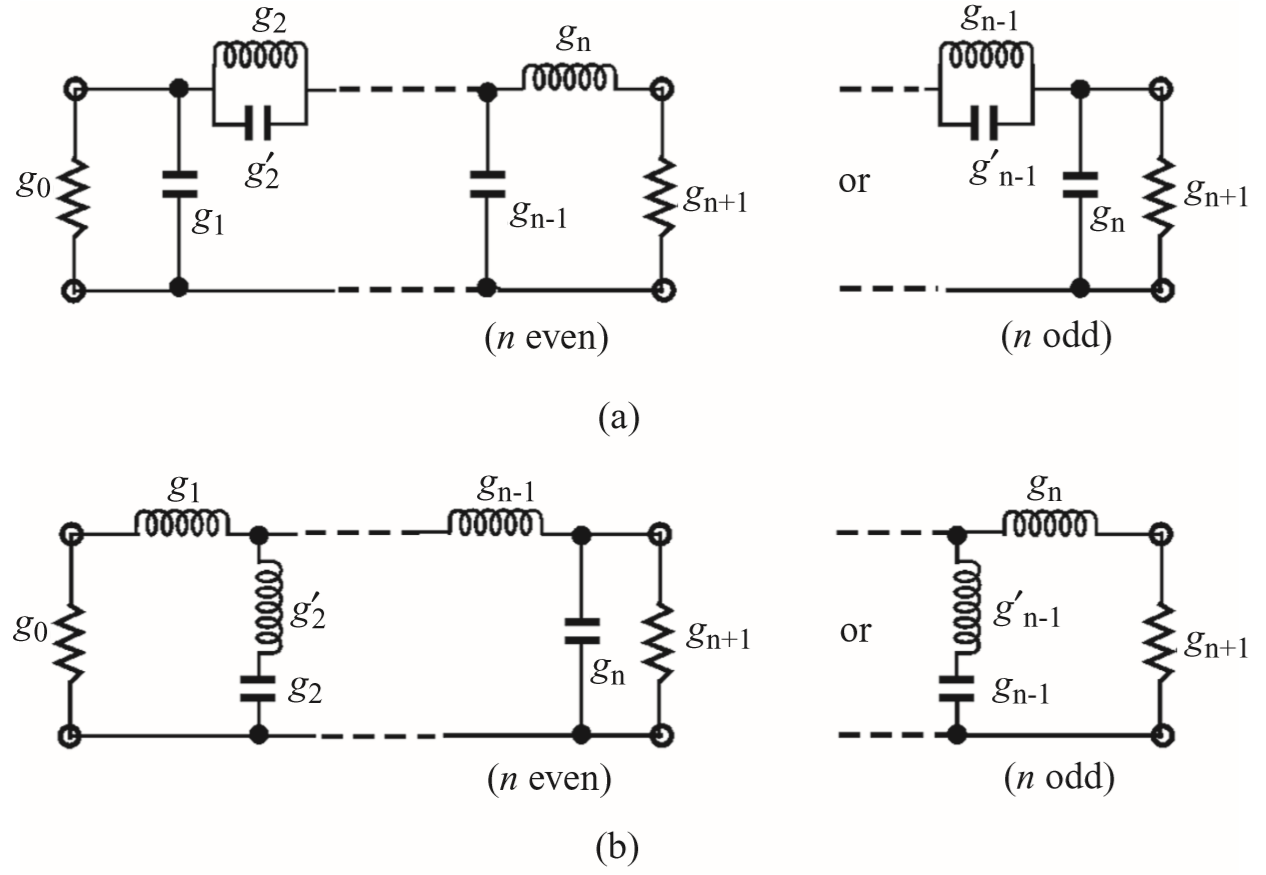

根据书中的原文内容，与Butterworth滤波器和Chebyshev滤波器不同，椭圆函数滤波器没有一个简易的公式来计算滤波器原型值。原文中给出了不同阶数下的设计参考值。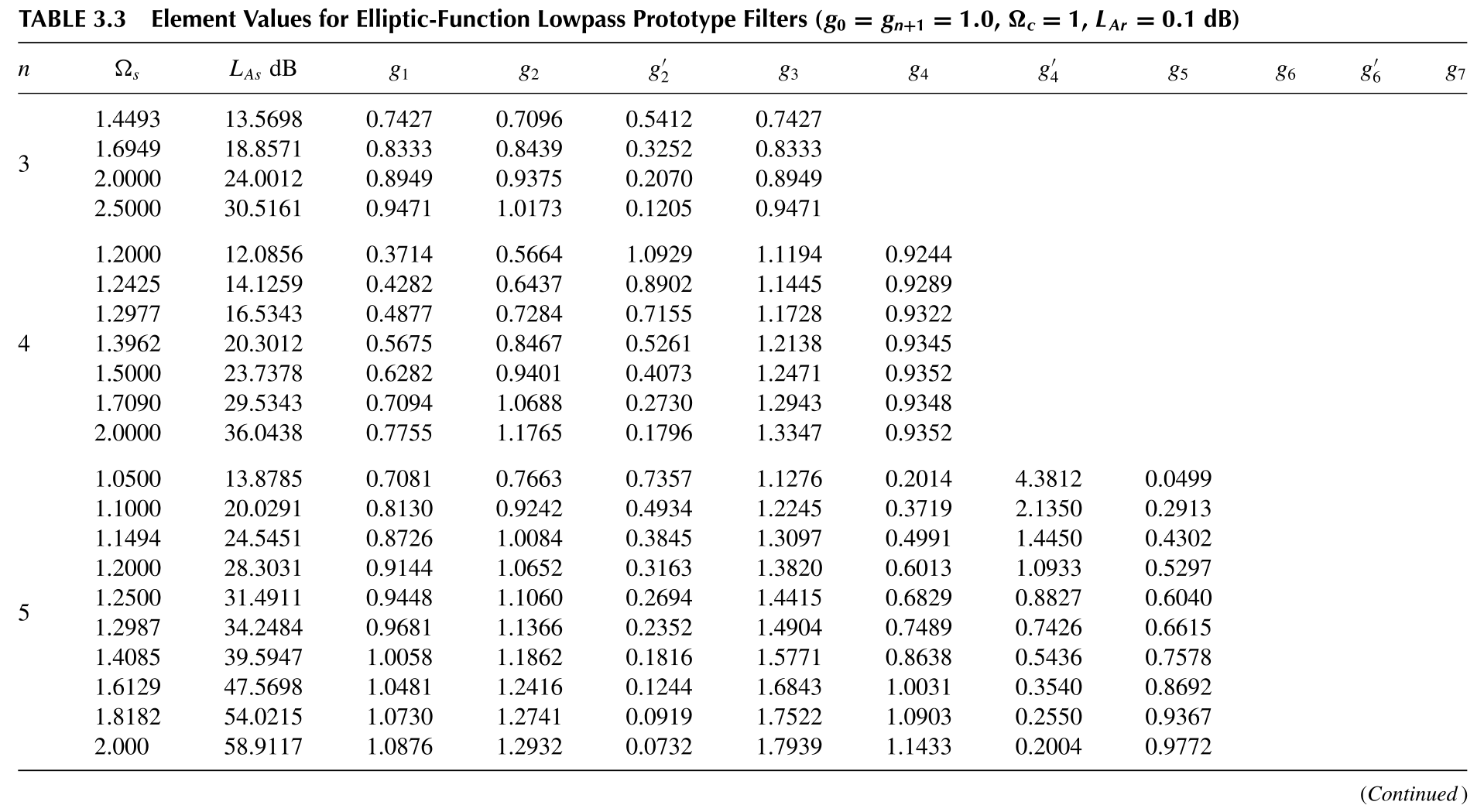


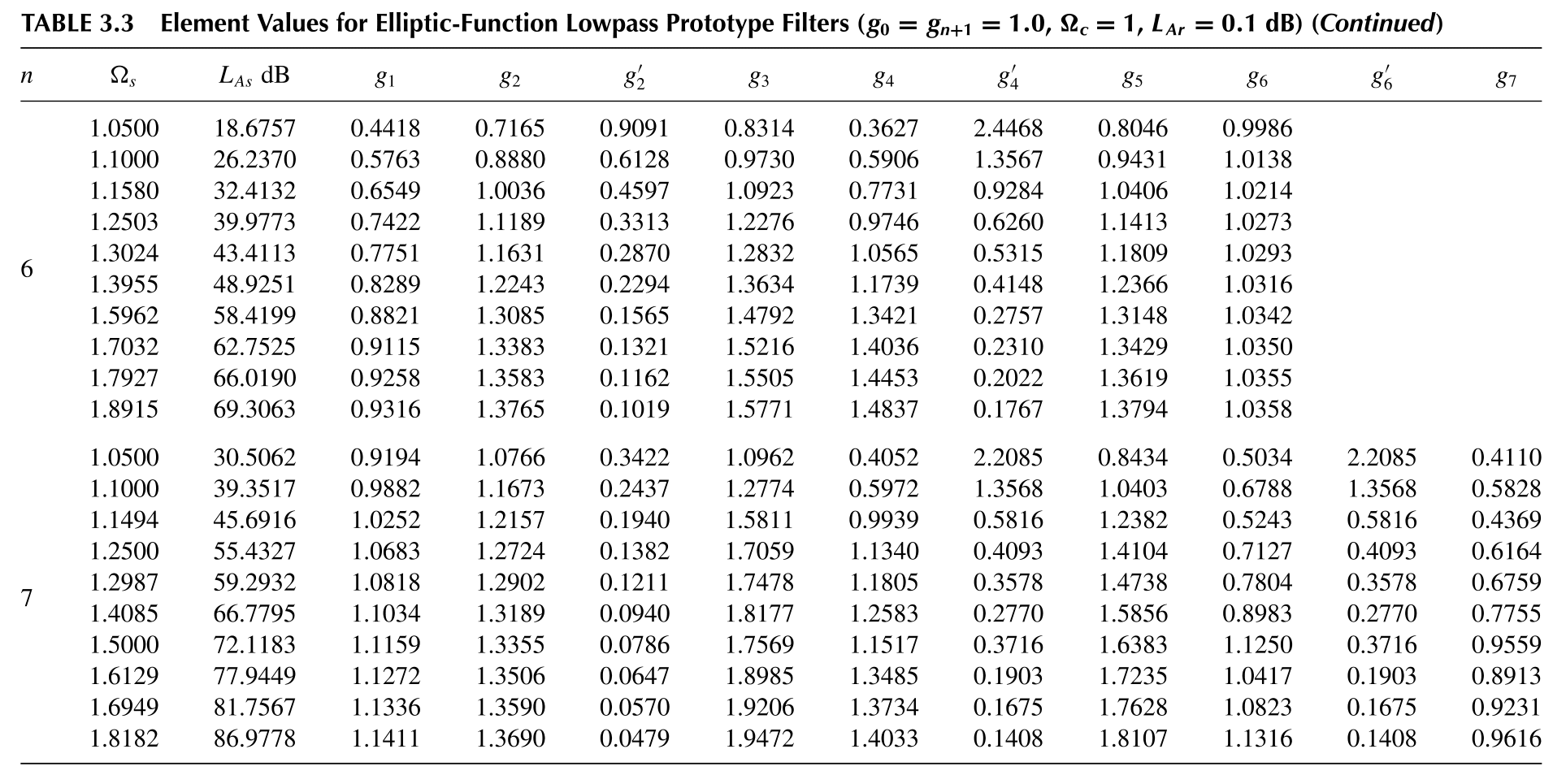
在设计时首先选择一个中心频率$\omega_c$，在设计时将其归一化为$\Omega_c=1$。表中所给的参考值的设计在通带内的插入损耗纹波$L_{Ar}=0.1dB$，通过选取通带外的插入损耗最小值$L_{As}$可以得到一组原型值，$L_{As}$越大可以得到越高的带外抑制水平，$L_{As}$越小可以得到越陡峭的过渡带，但是相应原型值的设计实现有可能会超出工艺限制。在$L_{As}$选定后，可以直接从表中得出通带第一次衰减到$L_{As}$水平时对应的归一化频率$\Omega_s$。

仿真设计和实验

原型仿真
以下以$n=5$、$L_{As}=24.5dB$为例，设置$f_c=5GHz$在确定$\omega_c$后，可用$$L_i=\frac{Z_0g_i}{\omega_c}$$和$$C_i=\frac{g_i}{Z_0\omega_c}$$分别计算电容和电感的值。
在ADS中设计原理图如下：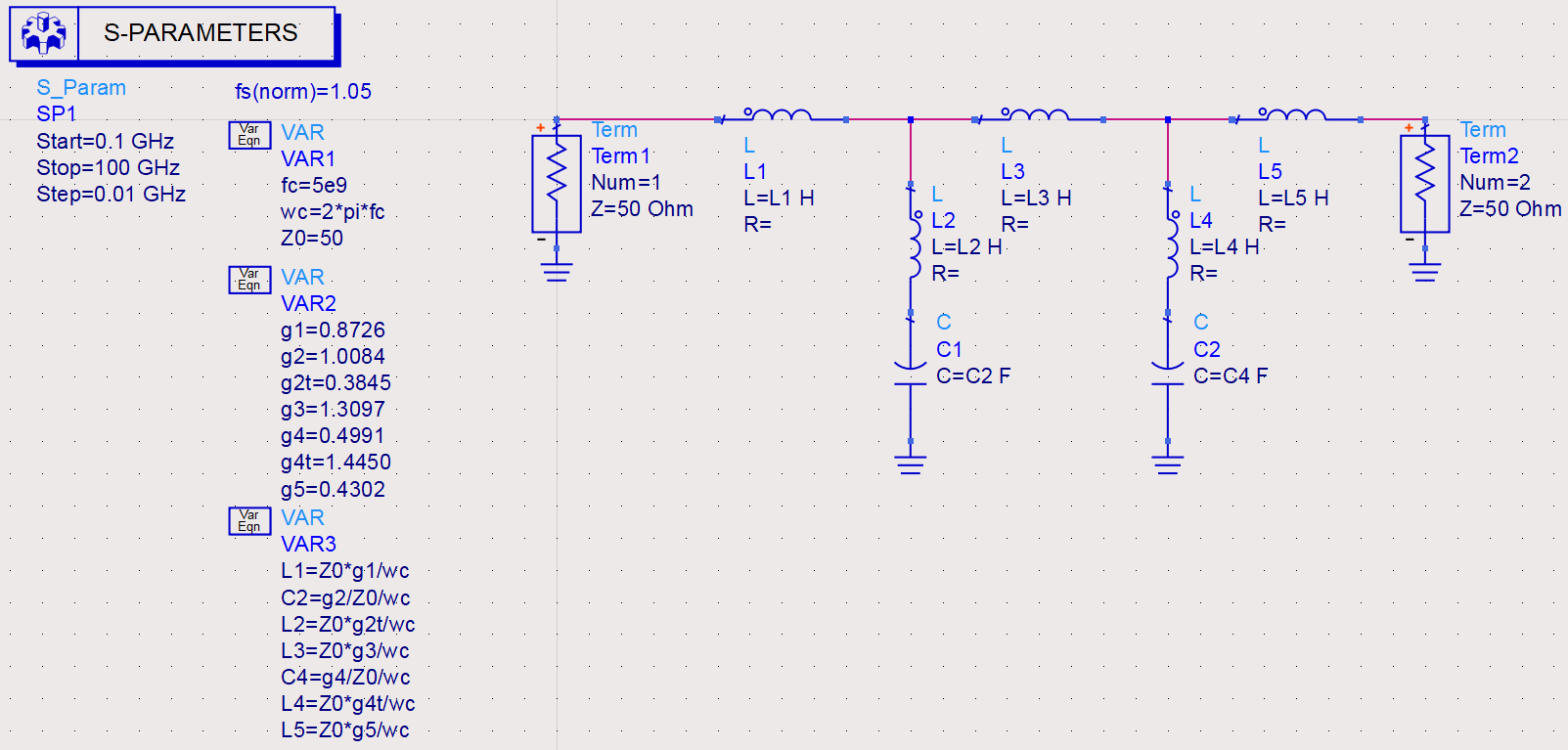

得到的通带附近的$S_{21}$随频率关系曲线如下：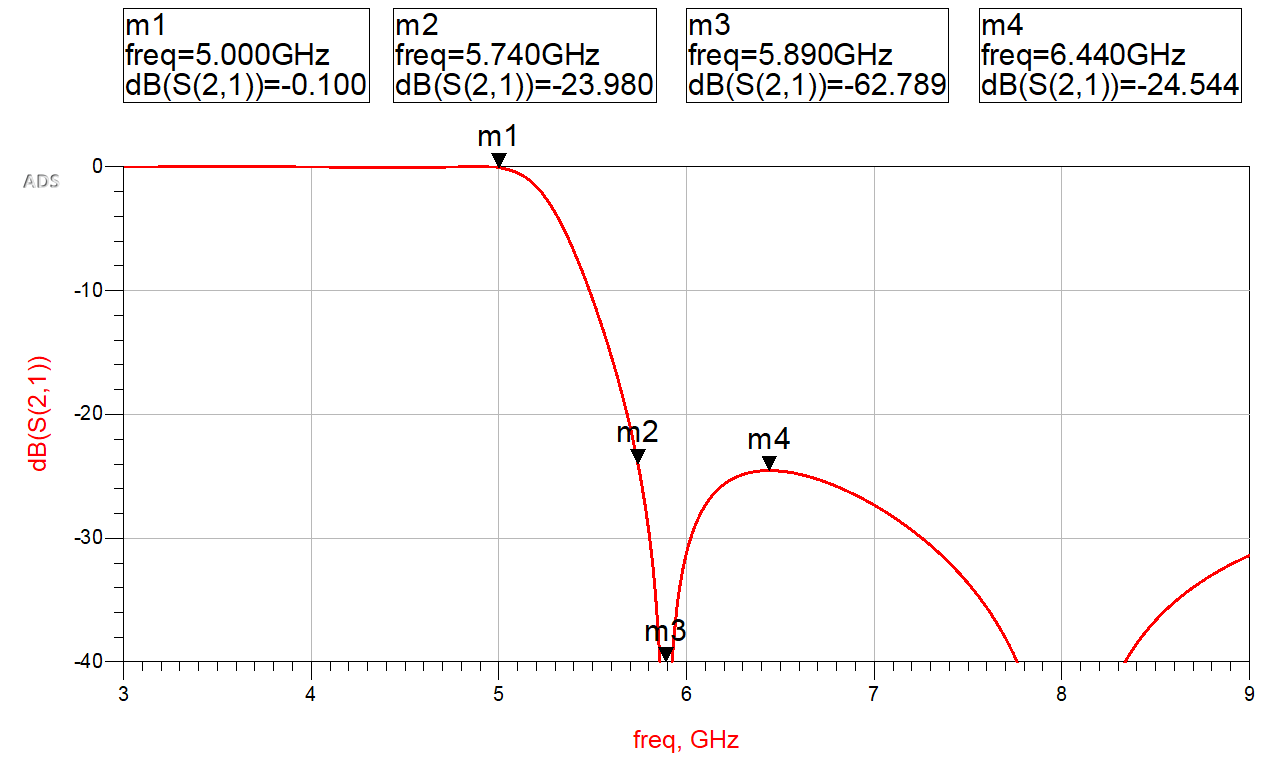

对数形式的回损和插损曲线如下：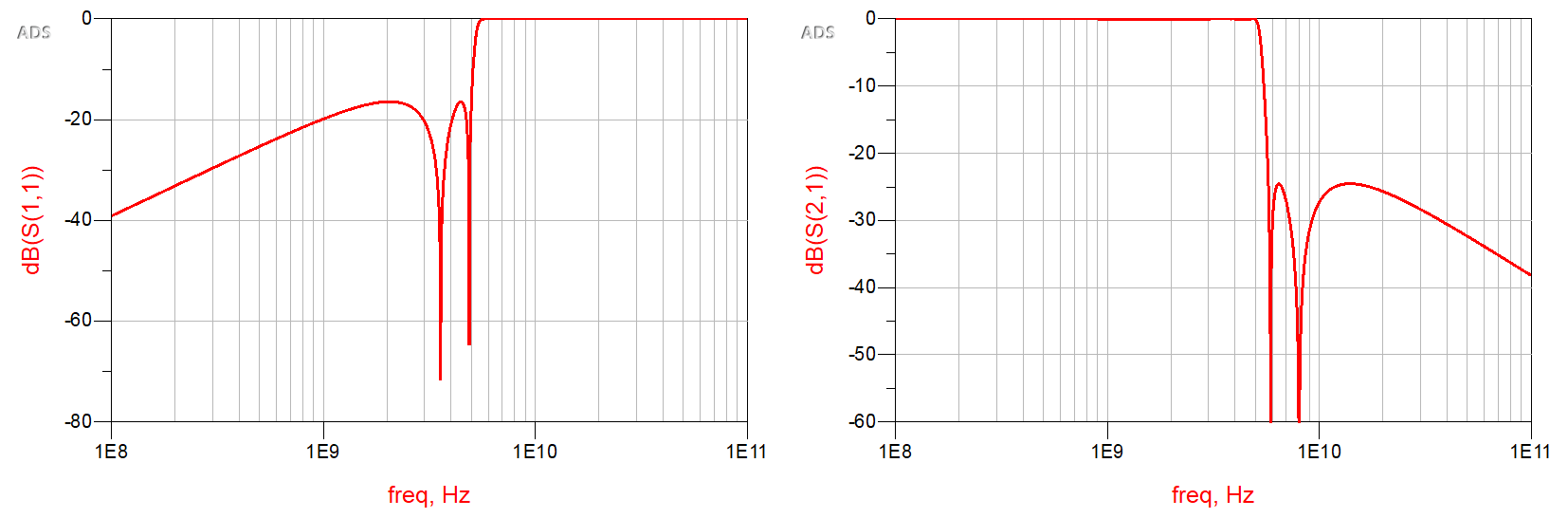

微带线仿真
此处使用RO5880基板（相对介电常数$\epsilon_r=2.2$，介电损耗$tan\delta=0.0009$，选取介质厚度$H=0.508mm$，选取铜厚$T=35\mu m$）进行仿真。选择容易制备的窄线阻抗$100\Omega$以等效串联电感，和尺寸不至于过宽的宽线阻抗$30\Omega$以等效接地电容，在$f_c=5GHz$时$100\Omega$阻抗线宽度为$0.409mm$，$50\Omega$馈线阻抗为$1.52mm$，$30\Omega$阻抗线宽度为$3.12mm$。
利用$$\beta l _L=\frac{Z_0 g}{Z_L}$$和$$\beta l _C=\frac{Z_C g}{Z_0}$$可以分别计算得到对应等效电感和等效电容的传输线的电长度（$rad/s$）。
金属层图形布局如下所示，其中，左右两侧各加入了一段5mm的馈线：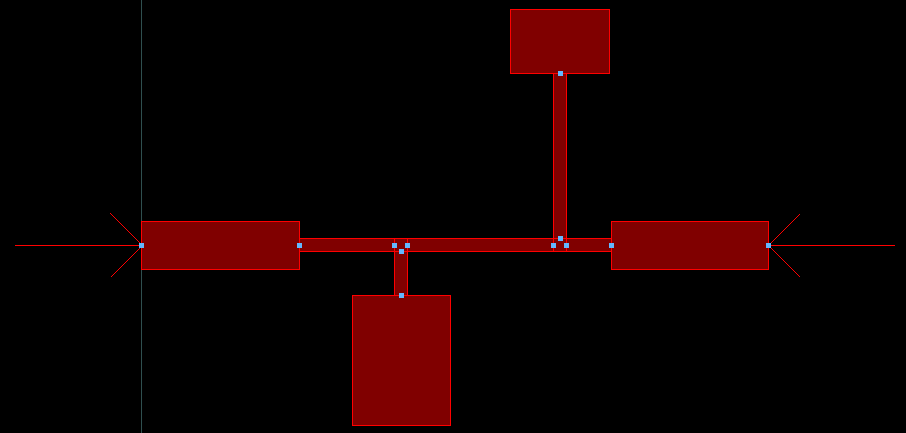

仿真结果如下：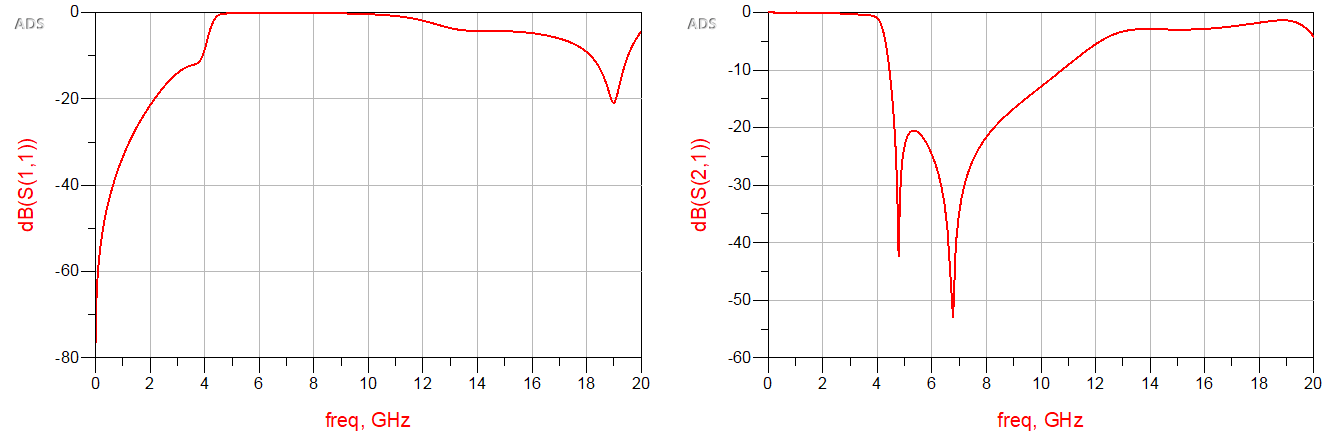

单从低通滤波器的特性上看，在通带右侧确实能得到较陡峭的过渡带，且在阻带存在两个零点。然而，该微带滤波器实现方式会引起频率特性的周期性重复，且直接计算得到的版图尺寸的仿真结果上看，$\omega_c$偏离了设计频率，需要进一步进行尺寸优化才能得到较为准确的$\omega_c$，此外，该实现方式得到的阻带峰值也略微高于理想情况下的阻带峰值。